Dark Energy Dynamics via the ISW Effect
From the last section, we saw that the ISW effect has the potential to verify or deny the existence of the dark energy from its induced temperature anisotropy in the CMB. The allure of such an effect derives not only from the fact that it is independent of the measurements made by Riess et. al. (1998) but also from its ability to probe the dynamics of the dark energy. In this section, we explore this possibility.
The "Size" of Dark Energy
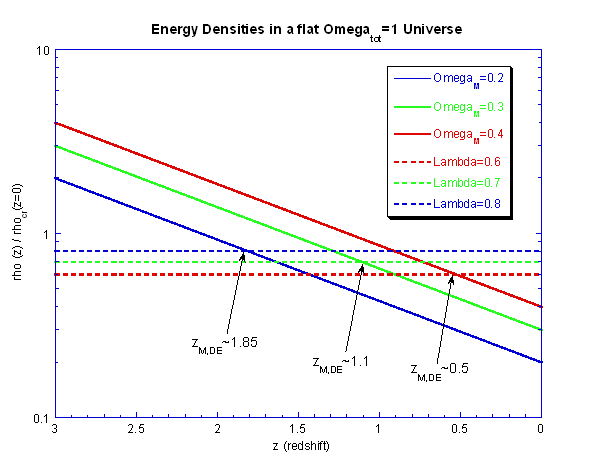
As Crittenden and Turok (1996) note, when modeling the dark energy as a cosmological constant Λ (as introduced before) and then allowing its value to increase, it comes to dominate the energy density at earlier and earlier times. This relationship is easily seen in the plot below. Here, we have simply taken the scale dependence on z (the redshift) for each energy component in the most recent epoch (0<z<3): ΩM~(1+z)3 and Λ is constant (note that what we have plotted here is the energy density for each component divided by the critical density today).

Additionally, Crittenden and Turok calculate the contribution to each Cl from the ISW integral prior to some cutoff redshift, zc, for a choice of ΩΛ=0.8 and h=0.7. Their results show that the most contribution is generated from z≤1, which is intuitively understandable since a that time ΩΛ is a few times ΩM.
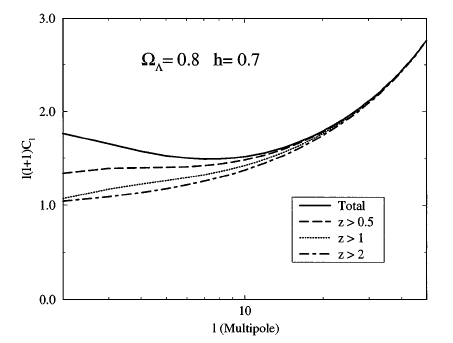
(Crittenden and Turok, 1996)
Very important to note, however, is what is not included in this plot: the statistical errors associated with the sample variance, the so-called cosmic variance. Explained extremely well by Kamionkowski & Loeb (1997) cosmic variance derives from the statistical nature of the effects one is trying to observe as they measure the CMB. In general, we would like to gain information regarding the primordial density perturbations whose effects we see as temperature fluctuations in the CMB. However, the process which we are observing 13 billions later was simply one realization of an essentially random process. To test a random process, we would like to be able to observe it as nearly to an infinite amount of times and then average over all realizations, similar to flipping a coin a million times and then averaging over how many times we say heads or tails. There is one catch: we only have 1 universe! So, for each scale l on the sky there are only (2l+1) realizations of that mode, and so there will thus be an error associated with this. In fact, for the lowest multipoles, the scale for which the ISW effect becomes the most important, the error associated with cosmic variance is the limiting factor in extracting information from the power spectrum of anisotropy. Despite this limitation, there are methods of subverting cosmic variance to which we will return in the next section.
From the above relationships we then see that the onset of a dark energy dominated universe depends significantly on its "size." The contribution made to the anisotropy power spectrum of the CMB is thus directly affected, even if only to a small degree. Therefore, the ISW anisotropy opens another window into the poorly understood passive characteristics of the dark energy such as its size and fractional contribution to the total energy density of the universe during the current epoch.
Dark Energy Speed of Sound
More than simply establishing the size of the dark energy, the ISW effect has the unique ability to probe its dynamics, and in particular we will focus here on its speed of sound. This facet of the dark energy is responsible for the possibility of clustering of the dark energy on scales below the horizon, and therefore on the evolution of fluctuations in the matter distribution. Following Bean and Doré (2003), one may adopt a phenomenological approach to the dark energy and model its properties as a cosmological fluid. An equation of state and a speed of sound are thus the fundamental parameters describing its dynamics and we will focus briefly on the latter.
For the perfect fluid assumption, the speed of sound in the fluid is completely described by the equation of state, which is itself merely a statement of the relationship between the density and pressure of the fluid. One may go on to show that the speed of sound and the equation of state of the dark energy affect the relative size of both the dark energy and dark matter density perturbations (see Bean and Doré 2003 for details). The significance of this consequence is fully dependent on the resulting signature in the CMB anisotropy spectrum. That is to say, since we are after phenomenological implications of the speed of sound of the dark energy, we will wish to judge its relative importance based on its observable effects.
From Hu (2001) a calculation of the contribution to each Cl from the ISW effect for two values of the sound speed shows that a decrease in the sound speed decreases the contribution from ISW to each Cl at low l.
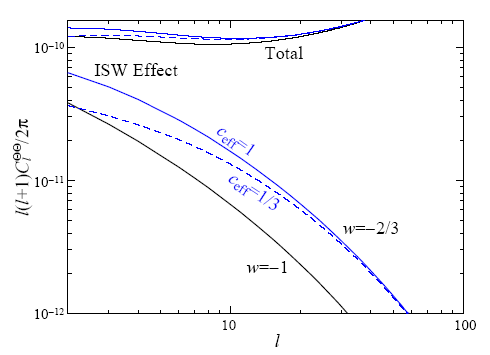
(Hu, 2001)
A similar calculation from Bean and Doré (2003), this time showing the full anisotropy spectrum from the CMB, obtains a similar result, this time showing the very large error bars associated with the cosmic variance.
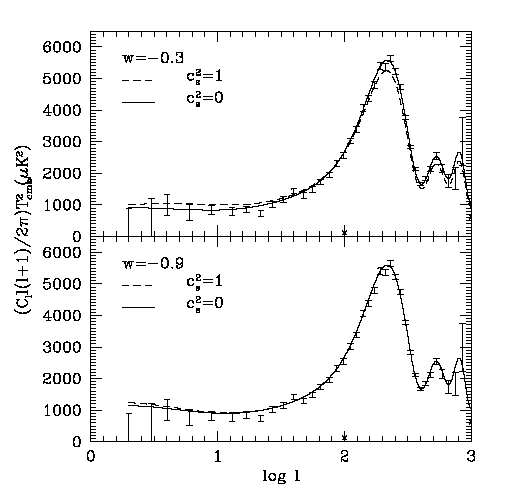
(Bean and Doré, 2003)
A few points to note here are that an increased sound speed of the dark energy increases the suppression of cold dark matter perturbations and therefore results in the increased power on large scales and that at low w, this suppression generates a contribution to the total power that is still dominated by the ISW effect. Moreover, since the ISW contribution to the anisotropy power spectrum occurs predominantly during very recent times, the effect is relatively independent of physics at high redshift (e.g. reionization).
As the authors (Bean and Doré) note, though, the cosmic variance limits the ability to place limits on this variation in the total anisotropy spectrum. For this reason other methods of extracting the ISW signal from the CMB have been developed, perhaps the most important and widely used being the cross-correlation of the CMB with the large-scale structure in the universe.
•