
The ISW Effect
We now have a coherent picture of the origin of the CMB anisotropy on almost all scales. At the surface of last scattering, when the photons in the photon-baryon plasma became too cool to keep the plasma ionized, acoustic oscillations that had been set up in the fluid via density and temperature fluctuations became temperature oscillations in the photons that free streamed to us today. Despite the seeming simplicity of this picture, there is yet another aspect to the signal we see today.
Introduction to Gravitational Potentials: Redshift and Blueshift
As the photons which left this surface of last scattering (SLS) nearly 14 billion years ago free stream toward an observer today they must pass through the intervening clusters of matter which have formed since. These clusters of matter include the familiar stars and galaxies as well as the less familiar dark matter and thus present to the path of the photon yet another source of gravitational potential.
As we have seen with the SW effect, the presence of a potential well in the path of a photon can induce a change in the energy, and thus the temperature, of the photon. As the photon encounters the lower potential associated with a massive object (like a galaxy cluster) it gains some amount of energy as it "falls into" the potential well (this is called a blueshift). However, the energy gained during infall into the potential is balanced by the energy lost as the photon climbs out the other side (this is called a redshift). This situation is quantitatively different from the SW effect described previously since in this case the potential well presented to the photon is localized to a single region along the path of the photons as they travel towards us from the SLS.

To gain a bit more insight into this idea, just imagine a marble rolling along a nice smooth surface until encounters a valley. As the marble rolls down into the valley it gains some speed, and thus gains some energy. As it rolls out the other side, however, it must "fight" gravity to climb up the other side and thus loses any extra energy that it gained on its way in. At the end of the marble's excursion it has the exact same speed (and thus energy) that it had before it rolled into the valley.
Under the most naive assumptions, the only component of the universe that will be involved in this process of gravitational blueshift and redshift will be the matter which is responsible for the gravitational potential in the first place: the dark matter and galaxies. This topic becomes complicated, however, due to the evolution of these large-scale structures over time, and more importantly, during the time that the photons from the SLS are traveling through the cosmos.
Is order to describe the effect of these large-scale structures on the photons, we need to to know something about how the gravitational potentials that they create evolve with time. To this end, we will now jump headfirst into the complications involved with the ISW effect, beginning with the fact that in a matter dominated universe where there is no smooth energy component, the so-called dark energy, gravitational potentials are constant (and thus the ISW effect is nonexistent).
From Einstein to Poisson: Constant Potentials
Following Hu & Eisenstein (1999) one can progress from Einstein's equations to a merely algebraic generalization of Poisson's equation which relates the background curvature, Newtonian curvature and density perturbation
![]() ,
,
where Φ is the Newtonian curvature and δρ is a density perturbation and K is the background curvature. Using this equation to relate the Newtonian curvature to the density perturbation we find that for the case where there is no dark energy
![]() .
.
Where, η is the conformal time coordinate used to track time in an expanding universe. Furthermore, we note that a gravitational potential gradient then leads to a bulk flow by
![]() ,
,
and that the divergence of this flow also leads to a density perturbation
![]() .
.
Thus, in the simple case of only clustering matter components, the gravitational potential associated with the clusters is a constant in time. More formally, this arises from the conservation of the Bardeen curvature ζ and then
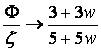
so that, indeed, Φ is a constant (since we assume w is also approximately constant over this time scale).
Potential Decay
Unfortunately, this is not the whole picture. There is now significant evidence for a non-trivial smooth energy component in the universe (Riess et al. 1998; Scranton et al. 2003). A dark energy component that does not cluster under the horizon scale impacts the evolution of gravitational potentials in a qualitatively different way than clustering energy and matter components.
Following a similar progression as that for matter clustering, one may derive the "equation of motion" for the evolution of the gravitational potential for which
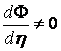 .
.
is now a solution and the constant potential is not. Physically, this effect is due to the contribution made by the smooth component to the potential while not contributing to the density perturbation. The solution that then follows for the potential decays away by approximately one factor of the scale factor.
The ISW Effect
Now that we have shown that in a universe containing dark energy gravitational potentials decay away, we have all of the conditions necessary for the integrated Sachs-Wolfe effect. As alluded to previously, this effect arises when the photons in the CMB traverse gravitational potentials in the large scale structure of the universe that vary with time and results in an additional temperature anisotropy beyond the ordinary Sachs-Wolfe effect. Let us begin by introducing the equations describing the magnitude of this effect and then we will discuss the implications of such a description.
The temperature anisotropy due to the ISW effect is given by an integral over the time variation of the gravitational potential
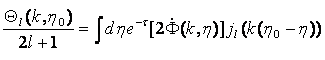
where the overdot indicates a conformal time derivative and Θ ≡ ΔT / T and the integral is taken over the line of sight to the last scattering surface. Due to the integral over the oscillating Bessel functions jl the dominant contribution to the CMB anisotropy will be on large scales. However, as Hu & Sugiyama (1994) point out, there will also be a significant relative contribution on small scales in a universe that becomes reionized at very early times. This relative contribution is due to cancellation in the Doppler and ordinary SW effects from opposite sides of a perturbation in the last scattering surface. Moreover, the ISW term will have a contribution at small scales with the same scale dependence as the canceled Doppler term. However, our universe seems to have reionized at much later times, and so this small scale contribution is washed out by the acoustic peaks in the CMB power spectrum.
The power spectrum of anisotropy produced is thus given by the usual methods and results in
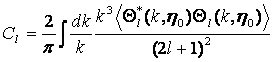
To make sense of the origin of the first integral and to understand why the dominant contribution from the ISW effect occurs at large scales (low multipole) recall the analogy made earlier between photons in potentials and balls on hill. If the ball must traverse several peaks and valleys, there is a greater tendency for the energy gained from falling into one potential well to be balanced by the need to climb up others. Similarly, if photons must traverse many density perturbations, which will generally be the case on small scales, then the fluctuations tend to cancel out along the line of sight, thus resulting in the slowly varying modes (the large scales again) contributing the most.
For a flat universe, the mechanism for this effect is the transition to a dark energy dominated expansion of the universe, such as might occur for cosmological constant (which is simply this dark energy which remains at a fixed value for all time). As Marc Kamionkowski pointed out (Kamionkowski 1996) when this effect arises in an open universe the cross-correltaion shanges. However, due to the recent emergence of a concordance model of the universe from recent measurements (WMAP, CBI, Ly-α, ACBAR, etc) it appears that the universe is very close to flat and so we will here focus on the consequences of the ISW effect in a flat universe. Therefore, observation of the ISW effect is an indicator of the presence of the mysterious dark energy.
•